Thoughts on applicability to our atmosphere
As we have discussed, Lorenz, in his celebrated paper, puts forth a simple model that describes the behavior of a layer of fluid that is warmer at the bottom than at the top. Such a layer is called a Rayleigh-Bénard layer, since Bénard and Rayleigh were the first to analyze such a layer around a century ago.
It turns out that although the model used by Lorenz provides a more-or-less reasonable description for fluid convection in a shallow layer of water sitting on a warm surface, it does not appear to provide a correct description for convection patterns occurring in the Earth's atmosphere, so that the atmospheric convection diagram shown on the second and succeeding slides is almost certainly incorrect when applied to the Earth's atmosphere. Below are a few thoughts that lead us to this conclusion.
The natural time unit used by Lorenz in his model,
which is the actual time T* elapsed when
his dimensionless time
variable τ increases by one unit, is given by the
expression
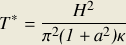
where H is the height of the fluid layer, a is the
ratio of the convection roll height to its width
(chosen by Lorenz to
be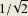 
; a is
the inverse of what is normally termed the aspect ratio),
and κ
is the thermal diffusivity of the fluid.
H2/κ is roughly the time taken for a thermal perturbation to propagate a distance H by thermal diffusion, so that in the Lorenz model, T* is roughly 1/15 of this time.
Other relevant parameters—properties of the fluid—include its kinematic viscosity ν (the ratio of the fluid viscosity to its density) and its volume thermal expansion coefficient β.
Two dimensionless parameters are particularly
relevant. They are the Prandtl number
σ = ν/κ, and
the Rayleigh number Ra.
In the Lorenz model (and in Rayleigh's analysis), the
Rayleigh number is given by the expression
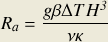
where g is the gravitational field strength.
Convection rolls develop when Ra exceeds
a critical value Rc , where
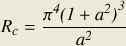
The minimum value of Rc , namely
27π4/4, occurs when
a2=1/2.
| Parameter | Air | Water |
|---|---|---|
| κ(m2/sec) | 2.1×10-5 | 1.5×10-7 |
| ν(m2/sec) | 1.5×10-5 | 9.8×10-7 |
| σ(ν/κ) | 0.7 | 6.5 |
| β(K-1) | 3.4×10-3 | 2.0×10-4 |
| T*(sec) | 3.2×103H2 | 4.5×105H2 |
| Ra | 1.1×108ΔT H3 | 1.3×1010ΔT H3 |
| Rc | 658 | 658 |
Here's a table that compares a layer of air with a layer of water, in terms of the various parameters above, all at 20°C:
Now in the Lorenz model, steady convection is always stable if the Prandtl number σ is less than 1+b. Since b is positive, the model cannot predict chaotic convection in our atmosphere, for which σ = 0.7.
Furthermore, for a layer of air only 1 meter high, the time scale T* for convection circulation is on the order of 3200 seconds, or nearly an hour. If we take H on the order of 104 meters (the scale height of the atmosphere), T* becomes approximately 10,000 years.
Finally, the value of the Rayleigh number Ra for the atmosphere, even for a layer only one meter high with the bottom only 0.1°C warmer than the top, is much larger than is appropriate for the Lorenz model. A value of Ra=107 would imply a value for Ra/Rc of over 15,000—beyond the range of applicability of the Lorenz model.
Clearly atmospheric convection phenomena cannot be appropriately described by this simple model.
On the other hand water, for which (at 20°C) σ = 6.5, may lie withing the model's range of applicability. For a layer of water 2 cm high, the value of T* is approximately 3 minutes (a reasonable time), and if ΔT = 1°C, the Rayleigh number Ra = 1.0×105, so that Ra/Rc = 158 (a reasonable number). Indeed, experiments have been done with water layers that show the existence of the convection rolls we have been discussing.
Generally speaking, the region of applicability for the Lorenz model is rather delicate, covering only a small range of ΔT. In order to observe the convection pattern of rolls in a pan of water that are described by the model, it is necessary to start with a very quiet water layer and heat it from the bottom uniformly and slowly. If one just puts a pot of water on the stove and turns on the burner in the normal way, those convection rolls will never have a chance to form.
In the case of the Earth's atmosphere it would be even more difficult, and not only for the reasons listed above. Too many other perturbations exist, stimulated by the Earth's rotation and by the large temperature differences spanning the Earth's surface, for example, between the equator and the polar regions—perturbations that give rise to the trade winds and the numerous cyclonic storms. However, Lorenz's comments about the unpredictability of our weather do not depend on whether his model is directly applicable to the atmosphere, since in the actual atmosphere, with its more turbulent behavior, any motion of the atmosphere must still be very sensitive to initial conditions. That is, the “butterfly effect” must still prevail.